Risk Aversion
Do human beings seek out risk or avoid it? How does risk affect behavior and what are the consequences for business and investment decisions? The answers to these questions lie at the heart of any discussion about risk. Individuals may be averse to risk but they are also attracted to it and different people respond differently to the same risk stimuli.
In this chapter, we will begin by looking at the attraction that risk holds to human beings and how it affects behavior. We will then consider what we mean by risk aversion and why it matters for risk management. We will follow up and consider how best to measure risk aversion, looking at a range of techniques that have been developed in economics. In the final section, we will consider the consequences of risk aversion for corporate finance, investments and valuation.
The Duality of Risk
In a world where people sky dive and bungee jump for pleasure, and gambling is a multi-billion dollar business, it is clear that human beings collectively are sometimes attracted to risk and that some are more susceptible to its attraction than others. While psychoanalysts at the beginning of the twentieth century considered risk-taking behavior to be a disease, the fact that it is so widespread suggests that it is part of human nature to be attracted to risk, even when there is no rational payoff to being exposed to risk. The seeds, it coud be argued, may have been planted in our hunter-gatherer days when survival mandated taking risks and there were no �play it safe� options.
At the same time, though, there is evidence that human beings try to avoid risk in both physical and financial pursuits. The same person who puts his life at risk climbing mountains may refuse to drive a car without his seat belt on or to invest in stocks, because he considers them to be too risky. As we will see in the next chapter, some people are risk takers on small bets but become more risk averse on bets with larger economic consequences, and risk-taking behavior can change as people age, become wealthier and have families. In general, understanding what risk is and how we deal with it is the first step to effectively managing that risk.
I am rich but am I happy? Utility and Wealth
While we can talk intuitively about risk and how human beings react to it, economists have used utility functions to capture how we react to at least economic risk. Individuals, they argue, make choices to maximize not wealth but expected utility. We can disagree with some of the assumptions underlying this view of risk, but it is as good a staring point as any for the analysis of risk. In this section, we will begin by presenting the origins of expected utility theory in a famous experiment and then consider possible special cases and issues that arise out of the theory.
The St. Petersburg Paradox and Expected Utility: The Bernoulli Contribution
Consider a simple experiment. I will flip a coin once and will pay you a dollar if the coin came up tails on the first flip; the experiment will stop if it came up heads. If you win the dollar on the first flip, though, you will be offered a second flip where you could double your winnings if the coin came up tails again. The game will thus continue, with the prize doubling at each stage, until you come up heads. How much would you be willing to pay to partake in this gamble?
This is the experiment that Nicholas Bernoulli proposed almost three hundred years ago, and he did so for a reason. This gamble, called the St. Petersburg Paradox, has an expected value of infinity but most of us would pay only a few dollars to play this game. It was to resolve this paradox that his cousin, Daniel Bernoulli, proposed the following distinction between price and utility:[1]
�� the value of an item must not be based upon its price, but rather on the utility it yields. The price of the item is dependent only on the thing itself and is equal for everyone; the utility, however, is dependent on the particular circumstances of the person making the estimate.�
Bernoulli had two insights that continue to animate how we think about risk today. First, he noted that the value attached to this gamble would vary across individuals, with some individuals willing to pay more than others, with the difference a function of their risk aversion. His second was that the utility from gaining an additional dollar would decrease with wealth; he argued that �one thousand ducats is more significant to a pauper than to a rich man though both gain the same amount�. He was making an argument that the marginal utility of wealth decreases as wealth increases, a view that is at the core of most conventional economic theory today. Technically, diminishing marginal utility implies that utility increases as wealth increases and at a declining rate.[2] Another way of presenting this notion is to graph total utility against wealth; Figure 2.1 presents the utility function for an investor who follows Bernoulli�s dictums, and contrasts it with utility functions for investors who do not.

If we accept the notion of diminishing marginal utility of wealth, it follows that a person�s utility will decrease more with a loss of $ 1 in wealth than it would increase with a gain of $ 1. Thus, the foundations for risk aversion are laid since a rational human being with these characteristics will then reject a fair wager (a 50% chance of a gain of $ 100 and a 50% chance of a loss of $100) because she will be worse off in terms of utility. Daniel Bernoulli�s conclusion, based upon his particular views on the relationship between utility and wealth, is that an individual would pay only about $ 2 to partake in the experiment proposed in the St. Petersburg paradox.[3]
While the argument for diminishing marginal utility seems eminently reasonable, it is possible that utility could increase in lock step with wealth (constant marginal utility) for some investors or even increase at an increasing rate (increasing marginal utility) for others. The classic risk lover, used to illustrate bromides about the evils of gambling and speculation, would fall into the latter category. The relationship between utility and wealth lies at the heart of whether we should manage risk, and if so, how. After all, in a world of risk neutral individuals, there would be little demand for insurance, in particular, and risk hedging, in general. It is precisely because investors are risk averse that they care about risk, and the choices they make will reflect their risk aversion. Simplistic though it may seem in hindsight, Bernoulli�s experiment was the opening salvo in the scientific analysis of risk.
Mathematics meets Economics: Von Neumann and Morgenstern
In the bets presented by Bernoulli and others, success and failure were equally likely though the outcomes varied, a reasonable assumption for a coin flip but not one that applies generally across all gambles. While Bernoulli�s insight was critical to linking utility to wealth, Von Neumann and Morgenstern shifted the discussion of utility from outcomes to probabilities.[4] Rather than think in terms of what it would take an individual to partake a specific gamble, they presented the individual with multiple gambles or lotteries with the intention of making him choose between them. They argued that the expected utility to individuals from a lottery can be specified in terms of both outcomes and the probabilities of those outcomes, and that individuals pick
one gamble over another based upon maximizing expected utility.
The Von-Neumann-Morgenstern arguments for utility are based upon what they called the basic axioms of choice. The first of these axioms, titledcomparability or completeness, requires that the alternative gambles or choices be comparable and that individuals be able to specify their preferences for each one. The second, termed transitivity, requires that if an individual prefers A to B and B to C, she has to prefer A to C. The third, referred to as the independence axiomspecifies that the outcomes in each lottery or gamble are independent of each other. This is perhaps the most important and the most controversial of the choice axioms. Essentially, we are assuming that the preference between two lotteries will be unaffected, if they are combined in the same way with a third lottery. In other words, if we prefer lottery A to lottery B, we are assuming that combining both lotteries with a third lottery C will not alter our preferences. The fourth axiom,measurability, requires that the probability of different outcomes within each gamble be measurable with a probability. Finally, the ranking axiom, presupposes that if an individual ranks outcomes B and C between A and D, the probabilities that would yield gambles on which he would indifferent (between B and A&D and C and A&D) have to be consistent with the rankings. What these axioms allowed Von Neumann and Morgenstern to do was to derive expected utility functions for gambles that were linear functions of the probabilities of the expected utility of the individual outcomes. In short, the expected utility of a gamble with outcomes of $ 10 and $ 100 with equal probabilities can be written as follows:
E(U) = 0.5 U(10) + 0.5 U(100)
Extending this approach, we can estimate the expected utility of any gamble, as long as we can specify the potential outcomes and the probabilities of each one. As we will see later in this chapter, it is disagreements about the appropriateness of these axioms that have animated the discussion of risk aversion for the last few decades.
The importance of what Von Neumann and Morgenstern did in advancing our understanding and analysis of risk cannot be under estimated. By extending the discussion from whether an individual should accept a gamble or not to how he or she should choose between different gambles, they laid the foundations for modern portfolio theory and risk management. After all, investors have to choose between risky asset classes (stocks versus real estate) and assets within each risk class (Google versus Coca Cola) and the Von Neumann-Morgenstern approach allows for such choices. In the context of risk management, the expected utility proposition has allowed us to not only develop a theory of how individuals and businesses should deal with risk, but also to follow up by measuring the payoff to risk management. When we use betas to estimate expected returns for stocks or Value at Risk (VAR) to measure risk exposure, we are working with extensions of Von Neumann-Morgenstern�s original propositions.
The Gambling Exception?
Gambling, whether on long shots on the horse track or card tables at the casinos, cannot be easily reconciled with a world of risk averse individuals, such as those described by Bernoulli. Put another way, if the St. Petersburg Paradox can be explained by individuals being risk averse, those same individuals create another paradox when they go out and bet on horses at the track or play at the card table since they are giving up certain amounts of money for gambles with expected values that are lower in value. Economists have tried to explain away gambling behavior with a variety of stories.
The first argument is that it is a subset of strange human beings who gamble and that that they cannot be considered rational. This small risk-loving group, it is argued, will only become smaller over time, as they are parted from their money. While the story allows us to separate ourselves from this unexplainable behavior, it clearly loses its resonance when the vast majority of individuals indulge in gambling, as the evidence suggests that they do, at least sometimes.
The second argument is that an individual may be risk averse over some segments of wealth, become risk loving over other and revert back to being risk averse again. Friedman and Savage, for instance, argued that individuals can be risk-loving and risk-averse at the same time, over different choices and for different segments of wealth: In effect, it is not irrational for an individual to buy insurance against certain types of risk on any given day and to go to the race track on the same day.[5] They were positing that we are all capable of behaving irrationally (at least relative to the risk averse view of the world) when presented with risky choices under some scenarios. Why we would go through bouts of such pronounced risk loving behavior over some segments of wealth, while being risk averse at others, is not addressed.
The third argument is that gambling cannot be compared to other wealth seeking behavior because individuals enjoy gambling for its own sake and that they are willing to accept the loss in wealth for the excitement that comes from rolling the dice. Here again, we have to give pause. Why would individuals not feel the same excitement when buying stock in a risky company or bonds in a distressed firm? If they do, should the utility of a risky investment always be written as a function of both the wealth change it creates and the excitement quotient?
The final and most plausible argument is grounded in behavioral quirks that seem to be systematic. To provide one example, individuals seem to routinely over estimate their own skills and the probabilities of success when playing risky games. As a consequence, gambles with negative expected values can be perceived (wrongly) to have positive expected value. Thus, gambling is less a manifestation of risk loving than it is of over confidence. We will return to this topic in more detail later in this chapter and the next one.
While much of the discussion about this topic has been restricted to individuals gambling at casinos and race tracks, it clearly has relevance to risk management. When a trader at a hedge fund puts the fund�s money at risk in an investment where the potential payoffs clearly do not justify the price paid, he is gambling, as is a firm that invests money into an emerging market project with sub-par cash flows. Rather than going through intellectual contortions trying to explain such phenomena in rational terms, we should accept the reality that such behavior is neither new nor unexpected in a world where some individuals, for whatever reason, are pre-disposed to risk seeking.
Small versus Large Gambles
Assume that you are offered a choice between getting $ 10 with certainty or a gamble, where you will make $21 with 50% probability and nothing the rest of the time; the expected value of the gamble is $10.50. Which one would you pick? Now assume that you are offered the choice between getting $10,000 with certainty or a gamble, where you will make $21,000 with 50% probability and nothing the rest of the time; the expected value of the gamble is $10,500. With conventional expected utility theory, where investors are risk averse and the utility function is concave, the answer is clear. If you would reject the first gamble, you should reject the second one as well.
In a famous paper on the topic, Paul Samuelson offered one of his colleagues on the economics department at MIT a coin flip where he would win $ 200 if he guessed right and lose $ 100 if he did not.[6] The colleague refused but said he would be willing to accept the bet if he was allowed one hundred flips with exactly the same pay offs. Samuelson argued that rejecting the individual bet while accepting the aggregated bet was inconsistent with expected utility theory and that the error probably occurred because his colleague had mistakenly assumed that the variance of a repeated series of bets was lower than the variance of one bet.
In a series of papers, Rabin challenged this view of the world. He showed that an individual who showed even mild risk aversion on small bets would need to be offered huge amounts of money with larger bets, if one concave utility function (relating utility to wealth) covered all ranges of his wealth. For example, an individual who would reject a 50:50 chance of making $ 11 or losing $10 would require a 50% chance of winning $20,242 to compensate for a 50% chance of losing $ 100 and would become infinitely risk averse with larger losses. The conclusion he drew was that individuals have to be close to risk neutral with small gambles for the risk aversion that we observe with larger gambles to be even feasible, which would imply that there are different expected utility functions for different segments of wealth rather than one utility function for all wealth levels. His view is consistent with the behavioral view of utility in prospect theory, which we will touch upon later in this chapter and return to in the next one.
There are important implications for risk management. If individuals are less risk averse with small risks as opposed to large risks, whether they hedge risks or not and the tools they use to manage those risks should depend upon the consequences. Large companies may choose not to hedge risks that smaller companies protect themselves against, and the same business may hedge against risks with large potential impact while letting smaller risks pass through to their investors. It may also follow that there can be no unified theory of risk management, since how we deal with risk will depend upon how large we perceive the impact of the risk to be.
Measuring Risk Aversion
If we accept Bernoulli�s proposition that it is utility that matters and not wealth per se, and we add the reality that no two human beings are alike, it follows that risk aversion can vary widely across individuals. Measuring risk aversion in specific terms becomes the first step in analyzing and dealing with risk in both portfolio and business contexts. In this section, we examine different ways of measuring risk aversion, starting with the widely used but still effective technique of offering gambles and observing what people choose to do and then moving on to more complex measures.
a. Certainty Equivalents
As we noted earlier, a risk-neutral individual will be willing to accept a fair bet. In other words, she will be willing to pay $ 20 for a 20% chance of winning $ 100 and a 80% chance of making nothing. The flip side of this statement is that if we can observe what someone is willing to pay for this bet (or any other where the expected value can be computed), we can draw inferences about their views on risk. A risk-averse individual, for instance, would pay less than $ 20 for this bet, and the amount paid will vary inversely with risk aversion.
In technical terms, the price that an individual is willing to pay for a bet where there is uncertainty and an expected value is called the certainty equivalent value. We can relate certainty equivalents back to utility functions. Assume that you as an individual are offered a choice between two risky outcomes, A and B, and that you can estimate the expected value across the two outcomes, based upon the probabilities, p and (1-p), of each occurring:
V = p A + (1-p) B
Furthermore, assume that you know how much utility you will derive from each of these outcomes and label them U(A) and U(B). If you are risk neutral, you will in effect derive the same utility from obtaining V with certainty as you would if you were offered the risky outcomes with an expected value of V:
For a risk neutral individual: U(V) = p U(A) + (1-p) U(B)
A risk averse individual, though, would derive much greater utility from the guaranteed outcome than from the gamble:
For risk averse individual: U(V) > p U(A) + (1-p) U(B)
In fact, there will be some smaller guaranteed amount (![]() ), which is labeled the certainty equivalent, that will provide the same utility as the uncertain gamble:
), which is labeled the certainty equivalent, that will provide the same utility as the uncertain gamble:
U(![]() ) = p U(A) + (1-p) U(B)
) = p U(A) + (1-p) U(B)
The difference between the expected value of the gamble and the certainty equivalent is termed the risk premium:
Risk Premium = V - ![]()
As the risk aversion of an individual increases, the risk premium demanded for any given risky gamble will also increase. With risk neutral individuals, the risk premium will be zero, since the utility they derive from the expected value of an uncertain gamble will be identical to the utility from receiving the same amount with certainty.
If this is too abstract, consider a very simple example of an individual with a log utility function. Assume that you offer this individual a gamble where he can win $ 10 or $100, with 50% probability attached to each outcome. The expected value of this gamble can be written as follows:
Expected Value = .50($10) + .50($100) = $ 55
The utility that this individual will gain from receiving the expected value with certainty is:
U(Expected Value) = ln($ 55) = 4.0073 units
However, the utility from the gamble will be much lower, sin
ce the individual is risk averse:
U(Gamble) = 0.5 ln($10) + 0.5 ln ($100) = 0.5(2.3026) +0.5(4.6051) = 3.4538 units
The certainty equivalent with therefore be the guaranteed value that will deliver the same utility as the gamble:
U(Certainty Equivalent) = ln(X) = 3.4538 units
Solving for X, we get a certainty equivalent of $31.62.[7] The risk premium, in this specific case is the difference between the expected value of the uncertain gamble and the certainty equivalent of the gamble:
Risk Premium = Expected value – Certainty Equivalent = $55 – $31.62 = $ 23.38
Using different utility functions will deliver different values for the certainty equivalent. Put another way, this individual should be indifferent between receiving $31.62 with certainty and a gamble where he will receive $ 10 or $ 100 with equal probability.
Certainty equivalents not only provide us with an intuitive way of thinking about risk, but they are also effective devices for extracting information from individuals about their risk aversion. As we will see in the next chapter, many experiments in risk aversion have been based upon making subjects choose between risky gambles and guaranteed outcomes, and using the choices to measure how their risk aversion. From a risk management perspective, it can be argued that most risk hedging products such as insurance and derivatives offer their users a certain cost (the insurance premium, the price of the derivative) in exchange for an uncertain cost (the expected cost of a natural disaster or movement in exchange rates) and that a significant subset of investors choose the certain equivalent.
b. Risk Aversion Coefficients
While observing certainty equivalents gives us a window into an individual�s views on risk, economists want more precision in risk measures to develop models for dealing with risk. Risk aversion coefficients represent natural extensions of the utility function introduced earlier in the chapter. If we can specify the relationship between utility and wealth in a function, the risk aversion coefficient measures how much utility we gain (or lose) as we add (or subtract) from our wealth. The first derivative of the utility function (dU/dW or U�) should provide a measure of this, but it will be specific to an individual and cannot be easily compared across individuals with different utility functions. To get around this problem, Pratt and Arrow proposed that we look at the second derivative of the utility function, which measures how the change in utility (as wealth changes) itself changes as a function of wealth level, and divide it by the first derivative to arrive at a risk aversion coefficient.[8] This number will be positive for risk-averse investors and increase with the degree of risk aversion.
Arrow-Pratt Absolute Risk Aversion = - U��(W)/U�(W)
The advantage of this formulation is that it can be compared across different individuals with different utility functions to draw conclusions about differences in risk aversion across people.
We can also draw a distinction between how we react to absolute changes in wealth (an extra $ 100, for instance) and proportional changes in wealth (a 1% increase in wealth), with the former measuring absolute risk aversion and the latter measuring relative risk aversion. Decreasing absolute risk aversion implies that the amount of wealth that we are willing to put at risk increases as wealth increases, whereas decreasing relative risk aversion indicates that the proportion of wealth that we are willing to put at risk increases as wealth increases. With constant absolute risk aversion, the amount of wealth that we expose to risk remains constant as wealth increases, whereas the proportion of wealth remains unchanged with constant relative risk aversion. Finally, we stand willing to risk smaller and smaller amounts of wealth, as we get wealthier, with increasing absolute risk aversion, and decreasing proportions of wealth with increasing relative risk aversion. In terms of the Arrow-Pratt measure, the relative risk aversion measure can be written as follows:
Arrow-Pratt Relative Risk Aversion = - W U��(W)/U�(W)
where,
W = Level of wealth
U�(W) = First derivative of utility to wealth, measuring how utility changes as wealth changes
U��(W) = Second derivative of utility to wealth, measuring how the change in utility itself changes as wealth changes
The concept can be illustrated using the log utility function.
U=ln(W)
U� = 1/W
U�� =1/W2
Absolute Risk Aversion Coefficient = U��/U� =W
Relative Risk Aversion Coefficient = 1
The log utility function therefore exhibits decreasing absolute risk aversion – individuals will invest larger dollar amounts in risky assets as they get wealthier – and constant relative risk aversion – individuals will invest the same percentage of their wealth in risky assets as they get wealthier. Most models of risk and return in practice are built on specific assumptions about absolute and relative risk aversion, and whether they stay constant, increase or decrease as wealth increases. Consequently, it behooves the users of these models to be at least aware of the underlying assumptions about risk aversion in individual utility functions. The appendix to this chapter provides a short introduction to the most commonly used utility functions in practice.
There is one final point that needs to be made in the context of estimating risk aversion coefficients. The Arrow-Pratt measures of risk aversion measure changes in utility for small changes in wealth and are thus local risk aversion measures rather than global risk aversion measures. Critics take issue with these risk aversion measures on two grounds:
- 1. The risk aversion measures can vary widely, for the same individual, depending upon how big the change in wealth is. As we noted in the discussion of small and large gambles in the utility section, there are some economists who note that individuals behave very differently when presented with small gambles (where less of their wealth is at stake) than with large gambles.
2. In a paper looking at conventional risk aversion measures, Ross argues that the Arrow-Pratt risk aversion axioms can yield counter-intuitive results, especially when individuals have to pick between two risky choices and provides two examples. In his first example, when two investors – one less risk averse (in the Arrow-Pratt sense) than the other – are presented with a choice between two risky assets, the less risk averse investor may actually invest less (rather than more) in the more risky asset than the more risk averse investor. In his second example, more risk averse individuals (again in the Arrow-Pratt sense) may pay less for partial insurance against a given risk than less risk averse individuals. The intuition he offers is simple: the Arrow-Pratt measures are too weak to be able to make comparisons across investors with different utility functions, when no risk free option alternative exists. Ross argues for a stronger version of the risk aversion coefficient that takes into account global differences.[9]
There is little debate about the proposition that measuring risk aversion is important for how we think about and manage risk but there remain two questions in putting the proposition into practice. The first is whether we can reliably estimate risk aversion coefficients when most individuals are unclear about the exact form and parameters of their utility functions, relative to wealth. The second is that whether the risk aversion coefficients, even if observable over some segment of wealth, can be generalized to cover all risky choices.
c. Other Views on Risk Aversion
All of the assessments of risk aversion that we have referenced hitherto in this chapter have been built around the proposition that it is expected utility that matters and that we can derive risk aversion measures by looking at utility functions. In the last few decades, there have been some attempts by researchers, who have been unconvinced by conventional utility theory or have been under whelmed by the empirical support for it, to come up with alternative ways of explaining risk aversion.
The Allais Paradox
The trigger for much of the questioning of the von Neumann-Morgenstern expected utility theory was the paradox exposited by the French economist, Maurice Allais, in two pairs of lottery choices.[10] In the first pair, he presented individuals with two lotteries – P1 and P2, with the following outcomes:
P1: $ 100 with certainty
P2: $0 with 1% chance, $100 with 89% chance, $500 with 10% chance
Most individuals, given a choice, picked P1 over P2, which is consistent with risk aversion. In the second pair, Allais offered these same individuals two other lotteries – Q1and Q2 with the following outcomes and probabilities:
Q1: $0 with 89% chance and $100 with 11% chance
Q2: $0 with 90% chance and $500 with 10% chance
Mathematically, it can be shown that an individual who picks P1 over P2 should pick Q1 over Q2 as well. In reality, Allais noted that most individuals switched, picking Q2 over Q1. To explain this paradox, he took issue with the Von Neumann-Morgenstern computation of expected utility of a gamble as the probability weighted average of the utilities of the individual outcomes. His argument was that the expected utility on a gamble should reflect not just the utility of the outcomes and the probabilities of the outcomes occurring, but also the differences in utilities obtained from the outcomes. In the example above, Q2 is preferred simply because the variance across the utilities in the two outcomes is so high.
In a closely related second phenomenon, Allais also noted what he called the common ratio effect. Given a choice between a 25% probability of making $ 8,000 and a 20% probability of making $ 10,000, Allais noted that most individuals chose the latter, in direct contradiction of the dictums of expected utility theory.[11] Both of the propositions presented by Allais suggest that the independence axiom on which expected utility theory is built may be flawed.
By pointing out that individuals often behaved in ways that were not consistent with the predictions of conventional theory, Allais posed a challenge to those who continued to stay with the conventional models to try to explain the discordant behavior. The responses to his paradox have not only helped advance our understanding of risk considerably, but pointed out the limitations of conventional expected utility theory. If as Allais noted, individuals collectively behave in ways that are not consistent with rationality, at least as defined by conventional expected utility theory, we should be cautious about using both the risk measurement devices that come out of this theory and the risk management implications.
Expected Utility Responses
The first responses to the Allais paradox were within the confines of the expected utility paradigm. What these responses shared in common was that they worked with von Neuman-Morgenstern axioms of choice and attempted to modify one or more of them to explain the paradox. In one noted example, Machina proposed that the independence axiom be abandoned and that stochastic dominance be used to derive what he termed �local expected utility� functions.[12] In intuitive terms, he assumed that individuals become more risk averse as the prospects become better, which has consequences for how we choose between risky gambles.[13] There is a whole family of models that are consistent with this reasoning and fall under the category of weighted utility functions, where different consequences are weighted differently (as opposed to the identical weighting given in standard expected utility models).
Loomes and Sugden relaxed the transitivity axiom in the conventional expected utility framework to develop what they called regret theory.[14] At its heart is the premise that individuals compare the outcomes they obtain within a given gamble and are disappointed when the outcome diverges unfavorably from what they might have had. Thus, large differences between what you get from a chosen action and what you could have received from an alternate action give rise to disproportionately large regrets. The net effect is that you can observe actions that are inconsistent with conventional expected utility theory.
There are other models that are in the same vein, insofar as they largely stay within the confines of conventional expected utility theory and attempt to explain phenomena such as the Allais paradox with as little perturbation to the conventional axioms as possible. The problem, though, is that these models are not always internally consistent and while they explain some of the existing paradoxes and anomalies, they create new paradoxes that they cannot explain.
Prospect Theory
While many economists stayed within the conventional confines of rationality and attempted to tweak models to make them conform more closely to reality, Kahneman and Tversky posed a more frontal challenge to expected utility theory.[15] As psychologists, they brought a very different sensibility to the argument and based their theory (which they called prospect theory) on some well observed deviations from rationality including the following:
a. Framing: Decisions often seem to be affected by how choices are framed, rather than the choices themselves. Thus, if we buy more of a product when it is sold at 20% off a list price of $2.50 than when it sold for a list price of $2.00, we are susceptible to framing. An individual may accept the same gamble he had rejected earlier, if the gamble is framed differently.
b. Nonlinear preferences: If an individual prefers A to B, B to C, and then C to A, he or she is violating one of the key axioms of standard preference theory (transitivity). In the real world, there is evidence that this type of behavior is not uncommon.
c. Risk aversion and risk seeking: Individuals often simultaneously exhibit risk aversion in some of their actions while seeking out risk in others.
d. Source: The mechanism through which information is delivered may matter, even if the product or service is identical. For instance, people will pay more for a good, based upon how it is packaged, than for an identical good, even though they plan to discard the packaging instantly after the purchase.
e. Loss Aversion: Individuals seem to fell more pain from losses than from equivalent gains. They note that individuals will often be willing to accept a gamble with uncertainty and an expected loss than a guaranteed loss of the same amount, in clear violation of basic risk aversion tenets.
Kahneman and Tversky replaced the utility function, which defines utility as a function of wealth, with a value function, with value defined as deviations from a reference point that allows for different functions for gains and losses. In keeping with observed loss aversion, for instance, the value function for losses was much steeper (and convex) than the value function for gains (and concave).
Figure 2.2: A Loss Aversion Function
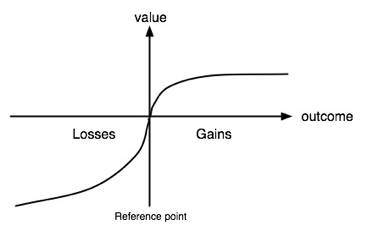
The implication is that how individuals behave will depend upon how a problem is framed, with the decision being different if the outcome is framed relative to a reference point to make it look like a gain as opposed to a different reference point to convert it into a loss. Stated in terms of risk aversion coefficients, they assumed that risk aversion coefficients behave very differently for upside than downside risk.
Kahneman and Tversky also offered an explanation for the Allais paradox in what they termed the common consequence effect. Their argument was that preferences could be affected by what they termed the consolation price effect, where the possibility of a large outcome can make individuals much more risk averse. This can be seen with the Allais paradox, where the expected utilities of the four lotteries can be written as follows:
E(u; P1) = 0.1u($100) + 0.89u($100) + 0.01u($100)
E(u; P2) = 0.1u($500) + 0.89u($100) + 0.01u($0)
E(u; Q1) = 0.1u($100) + 0.01u($100) + 0.89u($0)
E(u; Q2) = 0.1u($500) + 0.01u($0) + 0.89u($ 0)
Note that the common prize between the first pair of choices (P1 and P2) is 0.89 u($100), which is much larger than the common prize between the second pair of choices (Q1 and Q2) which is 0.89 u($0). With the higher common prize first pair, the individual is more risk averse than he is with the much lower common prize second pair.
If the earlier work by economists trying to explain observed anomalies (such as the Allais paradox) was evolutionary, Kahneman and Tversky�s work was revolutionary since it suggested that the problem with expected utility theory was not with one axiom or another but with its view of human behavior. The influence of Kahneman and Tversky on the way we view investments, in general, and risk specifically has been profound. The entire field of behavioral finance that attempts to explain the so-called anomalies in investor behavior has its roots in their work. It is also entirely possible that the anomalies that we find in risk management where some risks that we expect to see hedged do not get hedged and other risks that should not be hedged do, may be attributable to quirks in human behavior.
Consequences of Views on Risk
Now that we have described how we think about risk and measuring risk aversion, we should turn our attention to why it is of such consequence. In this section, we will focus on how risk and our attitudes towards it affect everything that we do as human beings, but with particular emphasis on economic choices from where we invest our money to how we value assets and run businesses.
a. Investment Choices
Our views of risk have consequences for how and where we invest. In fact, the risk aversion of an investor affects every aspect of portfolio design from allocating across different asset classes to selecting assets within each asset class to performance evaluation.
� Asset Allocation: Asset allocation is the first and perhaps the most important step in portfolio management, where investors determine which asset classes to invest their wealth in. The allocation of assets across different asset classes will depend upon how risk averse an investor is, with less risk averse investors generally allocating a greater proportion of their portfolios to riskier assets. Using the most general categorization of stocks, bonds and cash as asset classes, this would imply that less risk averse investors will have more invested in stocks than more risk averse investors, and that the most risk averse investors will not stray far from the safest asset class which is cash.[16]
� Asset Selection: Within each asset class, we have to choose specific assets to hold. Having decided to allocate specific proportions of a portfolio to stocks and bonds, the investor has to decide which stocks and bonds to hold. This decision is often made less complex by the existence of mutual funds of varying types from sector funds to diversified index funds to bond funds. Investors who are less risk averse may allocate more of their equity investment to riskier stocks and funds, though they may pay a price in terms of less than complete diversification.
� Performance Evaluation: Ultimately, our judgments on whether the investments we made in prior periods (in individual securities) delivered reasonable returns (and were therefore good investments) will depend upon how we measure risk and the trade off we demand in terms of higher returns.
The bottom line is that individuals are unique and their risk preferences will largely govern the right portfolios for them.
b. Corporate Finance
Just as risk affects how we make portfolio decisions as investors, it also affects decisions that we make when running businesses. In fact, if we categorize corporate financial decisions into investment, financing and dividend decisions, the risk aversion of decision makers feeds into each of these decisions:
� Investment Decisions: Very few investments made by a business offer guaranteed returns. In fact, almost every investment comes with a full plate of risks, some of which are specific to the company and sector and some of which are macro risks. We have to decide whether to invest in these projects, given the risks and our expectations of the cashflows.
� Financing Decisions: When determining how much debt and equity we should use in funding a business, we have to confront fundamental questions about risk and return again. Specifically, borrowing more to fund a business may increase the potential upside to equity investors but also increase the potential downside and put the firm at risk of default. How we view this risk and its consequences will be central to how much we borrow.
� Dividend Decisions: As the cash comes in from existing investments, we face the question of whether to return some or a lot of this cash to the owners of the business or hold on to it as a cash balance. Since one motive for holding on to cash is to meet contingencies in the future (an economic downturn, a need for new investment), how much we choose to hold will be determined by how we perceive the risk of these contingencies.
While these are questions that every business, private and public, large and small, has to answer, an additional layer of complexity is added when the decision makers are not the owners of the business, which is all too often the case with publicly traded firms. In these firms, the managers who make investment, financing and dividend decisions have very different perspectives on risk and reward than the owners of the business. Later in this book, we will return to this conflict and argue that it may explain why so many risk management products, which are peddled to the managers and not to the owners, are directed towards hedging risk and not exploiting it.
c. Valuation
In both portfolio management and corporate finance, the value of a business underlies decision-making. With portfolio management, we try to find companies that trade at below their �fair� value, whereas in corporate finance, we try to make decisions that increase firm value. The value of any asset or collection of assets (which is what a business is) ultimately will be determined by the expected cash flows that we expect to generate and the discount rate we apply to these cash flows. In conventional valuation, risk matters primarily because it determines the discount rate, with riskier cash flows being discounted at higher rates.
We will argue that this is far too narrow a view of risk and that risk affects everything that a firm does, from cash flows to growth rates to discount rates. A rich valuation model will allow for this interplay between how a firm deals with risk and its value, thus giving us a tool for evaluating the effects of all aspects of risk management. It is the first step in more comprehensive risk management.
Conclusion
As human beings, we have decidedly mixed feelings about risk and its consequences. On the one hand, we actively seek it out in some of our pursuits, sometimes with no rewards, and on the other, we manifest a dislike for it when we are forced to make choices. It is this duality of risk that makes it so challenging.
In this chapter, we considered the basic tools that economists have devised for dealing with risk. We began with Bernoulli�s distinction between price and utility and how the utility of a wager will be person-specific. The same wager may be rejected by one person as unfair and embraced by another as a bargain, because of their different utility functions. We then expanded on this concept by introducing the notion of certainty equivalents (where we looked at the guaranteed alternative to a risky outcome) and risk aversion coefficients (which can be compared across individuals). While economists have long based their analysis of risk on the assumptions of rationality and diminishing marginal utility, we also presented the alternative theories based upon the assumptions that individuals often behave in ways that are not consistent with the conventional definition of rationality.
In the final part of this chapter, we examined why measuring and understanding risk is so critical to us. Every decision that we are called upon to make will be colored by our views on risk and how we perceive it. Understanding risk and how it affects decision makers is a prerequisite of success in portfolio management and corporate finance.
Appendix: Utility Functions and Risk Aversion Coefficients
In the chapter, we estimated the absolute and relative risk aversion coefficients for the log utility function, made famous by Bernoulli�s use of it to explain the St. Petersburg paradox. In fact, the log utility function is not the only one that generates decreasing absolute risk aversion and constant relative risk aversion. A power utility function, which can be written as follows, also has the same characteristics.
U(W) = Wa
Absolute risk aversion =
Relative risk aversion =
Figure 2A.1 graphs out the log utility and power utility functions for an individual:
Figure 2A.1: Log Utility and Power Utility Functions

There are other widely used functions that generate other combinations of absolute and relative risk aversion. Consider, for instance, the exponential utility function, which takes the following form:
U(W) = a- exp-bW
Absolute risk aversion =
Relative risk aversion =
This function generates constant absolute risk aversion (where individuals invest the same dollar amount in risky assets as they get wealthier) and increasing relative risk aversion (where a smaller percentage of wealth is invested in risky assets as wealth increases). Figure 2A.2 graphs out an exponential utility function:
Figure 2A.2: Exponential Utility Function

The quadratic utility function has the very attractive property of linking the utility of wealth to only two parameters – the expected level of wealth and the standard deviation in that value.
U(W) = a+ bW – c W2
Absolute risk aversion =
Relative risk aversion =
The function yields increasing absolute risk aversion, where investors invest less of their dollar wealth in risky assets as they get wealthier, a counter intuitive result. Figure 2A.3 graphs out a quadratic utility function:
Figure 2A.3: Quadratic Utility Functiion

Having described functions with constant and increasing relative risk aversion, consider a final example of a utility function that takes the following form:
U(W) = ![]() (with g>0)
(with g>0)
Absolute risk aversion =
Relative risk aversion =
This function generates decreasing relative risk aversion, where the proportion of wealth invested in risky assets increases as wealth increases.
The functions described in this appendix all belong to a class of utility functions called Hyperbolic Absolute Risk Aversion or HARA functions. What these utility functions share in common is that the inverse of the risk aversion measure (also called risk tolerance) is a linear function of wealth.
While utility functions have been mined by economists to derive elegant and powerful models, there are niggling details about them that should give us pause. The first is that no single utility function seems to fit aggregate human behavior very well. The second is that the utility functions that are easiest to work with, such as the quadratic utility functions, yield profoundly counter intuitive predictions about how humans will react to risk. The third is that there are such wide differences across individuals when it comes to risk aversion that finding a utility function to fit the representative investor or individual seems like an exercise in futility. Notwithstanding these limitations, a working knowledge of the basics of utility theory is a prerequisite for sensible risk management.
[1] Bernoulli, D., 1738, Exposition of a New Theory on the Measurement of Risk. Translated into English in Econometrica, January 1954. Daniel came from a family of distinguished mathematicians and his uncle, Jakob, was one of the leading thinkers in early probability theory.
[2] In more technical terms, the first derivative of utility to wealth is positive while the second derivative is negative.
[3] Bernoulli proposed the log utility function, where U(W) = ln(W). As we will see later in this chapter, this is but one in a number of utility functions that exhibit diminishing marginal utility.
[4] Von Neumann, J. and O. Morgenstern (1944) Theory of Games and Economic Behavior. 1953 edition, Princeton, NJ: Princeton University Press.
[5] Friedman, M. and L.P. Savage (1948) "The Utility Analysis of Choices involving Risk", Journal of Political Economy, Vol. 56, p.279-304. They developed a utility function that was concave (risk averse) for some segments of wealth and convex (risk loving) over others.
[6] Samuelson, P. 1963. �Risk and Uncertainty: A Fallacy of Large Numbers.� Scientia. 98, pp. 108-13.
[7] To estimate the certainty equivalent, we compute exp(3.4538) = 31.62
[8] Pratt, J.W., 1964, Risk Aversion in the Small and the Large, Econometric, v32, pg 122-136; Arrow, K., 1965, Aspects of the Theory of Risk-Bearing. Helsinki: Yrj� Hahnsson Foundation.
[9] Ross, S.A., 1981, Some Stronger Measures of Risk Aversion in the Small and in the Large with Applications, Econometrica, Vol. 49 (3), p.621-39.
[10] Allais, M. 1979, The So-Called Allais Paradox and Rational Decisions under Uncertainty", in Allais and Hagen, Expected Utility Hypotheses and the Allais Paradox. Dordrecht: D. Reidel.
[11] The two gambles have the same expected value of $ 2000, but the second gamble is more risky than the first one. Any risk averse individual who obeys the dictums of expected utility theory would pick the first gamble.
[12] Machina, Mark J. 1982. ��Expected Utility� Theory without the Independence Axiom,� Econometrica, 50, pp. 277–323. Stochastic dominance implies that when you compare two gambles, you do at least as well or better under every possible scenario in one of the gambles as compared to the other.
[13] At the risk of straying too far from the topic at hand, indifference curves in the Von-Neumann-Morgenstern world are upward sloping and parallel to each other and well behaved. In the Machina�s modification, they fan out and create the observed Allais anomalies.
[14] Loomes, Graham and Robert Sugden. 1982. �Regret Theory: An Alternative Theory of Rational Choice under Uncertainty,� Econ. J. 92, pp. 805–24.
[15] Kahneman, D. and A. Tversky, 1979, Prospect Theory: An Analysis of Decision under Risk, Econometrica, v47, 263-292.
[16] Cash includes savings accounts and money market accounts, where the interest rates are guaranteed and there is no or close to no risk of losing principal.
No comments:
Post a Comment